「数学はセンスだ」と思っていませんか? それは大きな誤解です。数学は「センス」だけではなく「正しい順序で積み上げたレンガの高さ」でも決まります。
やみくもに難問に挑んでも、基礎がスカスカなら必ず崩れます。 今回は、王道のロードマップを紹介します。 全てのステップで「3周」し、セルフレクチャーで仕上げる。そして、分野ごとに立ち止まらず、全体を何度も塗り重ねる。この「回転数」こそが、あなたの数学力を劇的に変えます。
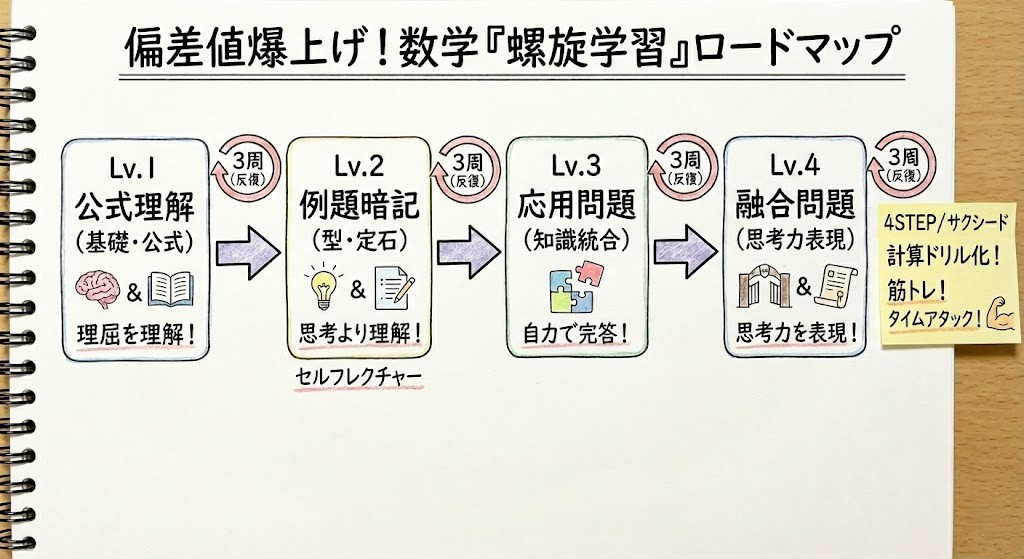
戦略データ:学習の全体像「全体螺旋」とは?
まず、最も重要なマインドセットを変えましょう。「二次関数を完璧にしてから三角比へ…」という「単元ごとの深掘り」はNGです。完璧主義は挫折の元です。正解は、「数学全体のレベル1を終わらせてから、レベル2へ進む」という「全体螺旋(スパイラル)学習」です。
【学習サイクルのイメージ】
- 1周目(Lv.1 基礎): 数学全体の基礎(教科書・基本例題)を終わらせる。
- 2周目(Lv.2 標準): 数学全体の標準(重要例題・標準演習)を終わらせる。
- 3周目(Lv.3 応用): 数学全体の応用(入試問題)に挑む。
薄い塗装を何度も重ねるように、全体を高速で回転させることで、単元間のつながりが見え、忘れにくくなります。
ステップ1:全ての始まり【基本事項・公式の理解】
全ての土台です。教科書や講義系参考書(「入門問題精講」など)を読み、概念を理解します。
【攻略の鉄則】
- 目標周回数:3周
- 1周で全て理解しようとせず、3周読んで「なるほど」を増やしていきます。
- 公式は「証明」する
- 例えば「判別式 D=b^2-4ac」をただ暗記してはいけません。「なぜこの式で解の個数がわかるのか?」を、解の公式から導けるようにしてください。この「理屈」が、応用問題での武器になります。
ステップ2:解法の”型”を学ぶ【例題・解法暗記】
「Super Quick」などの「例題」を使い、数学の「定石(型)」をインプットします。
【攻略の鉄則】
- 目標周回数:3周(セルフレクチャー)
- 1周目: 5分考えて分からなければすぐ答えを見る。「思考」よりも「理解」優先。
- 2周目: 手を動かして解く。「再現」できるか確認する。
- 3周目: 「セルフレクチャー」を行う。問題を見て、解法の手順を瞬時に説明できて初めてクリア。
ステップ3:知識を統合する【標準・応用問題演習】
ステップ2で入れた「型」を組み合わせ、初見の問題を解く訓練です。『文系の数学 重要事項完全習得編』などが該当します。
【攻略の鉄則】
- 目標周回数:3周
- 1周目: ヒントなしで10分粘る。解けなければ解説を熟読し、どこで詰まったか(知識不足か、発想不足か)を分析する。
- 2周目: 翌日以降、自力で完答できるか試す。
- 3周目: 期間を空けて再トライ。「瞬殺」できるレベルに仕上げる。
ステップ4:思考力を表現する【過去問・融合問題】
サイクルの総仕上げです。志望校の過去問や、複数の単元が絡む融合問題に挑みます。問題集では、「ゴールデンルート 数学1A・2B 応用編」などが該当します。
【攻略の鉄則】
- 目標周回数:3周(復習重視)
- 「解いて採点して終わり」ではありません。なぜその発想に至るのか、別解はないか、徹底的に研究するために3回解き直します。勿論、3周目にはセルフレクチャーができることが必須です。
- AI添削を活用する
- 記述答案は、ChatGPTなどの生成AIに「この証明で論理の飛躍はある?」と聞いてみてください。自分では気づけない減点ポイントを指摘してくれます。
コラム:学校の「4STEP」「サクシード」はゴミか?
ネット上では「解説が不親切」「やるだけ無駄」と酷評されがちな、学校配布の教科書傍用問題集(4STEP、サクシード、クリアーなど)。 確かに、これで「解法を学ぼう」とするのは効率が悪すぎます。しかし、使い方を工夫すれば最強の武器になります。
結論:「計算ドリル」だと思え。
大学入試で落ちる受験生の多くは難問が解けなくて落ちるのではなく、「典型問題での計算ミス」や「計算スピードの遅さ」で落ちます。この「計算力(基礎体力)」を鍛えるには、4STEPのような大量の反復練習が最適です。
- 思考力は他の参考書や問題集で鍛える。
- 計算力は「教科書傍用問題集」で鍛える。
「これは筋トレだ」と割り切り、タイムアタック形式で解きまくる。その用途においては、これ以上の教材はありません。
まとめ:立ち止まらず、全体を回せ
数学学習のロードマップをまとめます。
- 単元ごとに立ち止まらず、数IA・数IIBCなどの「全範囲」を薄く何度も塗る。
- 全てのステップで「3周」し、脳への定着を確実にする。
- 「セルフレクチャー」で、解法の検索スピードを極限まで上げる。
- 学校の問題集は「計算筋トレ」として利用する。
一つの単元で沼にハマってはいけません。螺旋階段を登り続けてください。3周目が終わる頃、あなたの数学力は別次元に到達しています。




コメント