「MARCH・関関同立を志望しているが、数学で足を引っ張りたくない」 「基礎はある程度できたつもりだが、難関大の入試問題になると歯が立たない」
本記事では、文系数学でMARCH(明治・青山・立教・中央・法政)や関関同立(関西・関西学院・同志社・立命館)の合格点を確実に取るための学習ルートを公開します。
現状の学力(全統模試の偏差値を目安)に合わせて3つのスタート地点を設定しました。このルートは単なる「解法暗記」ではなく、難関大特有の「思考力」を養うための設計になっています。
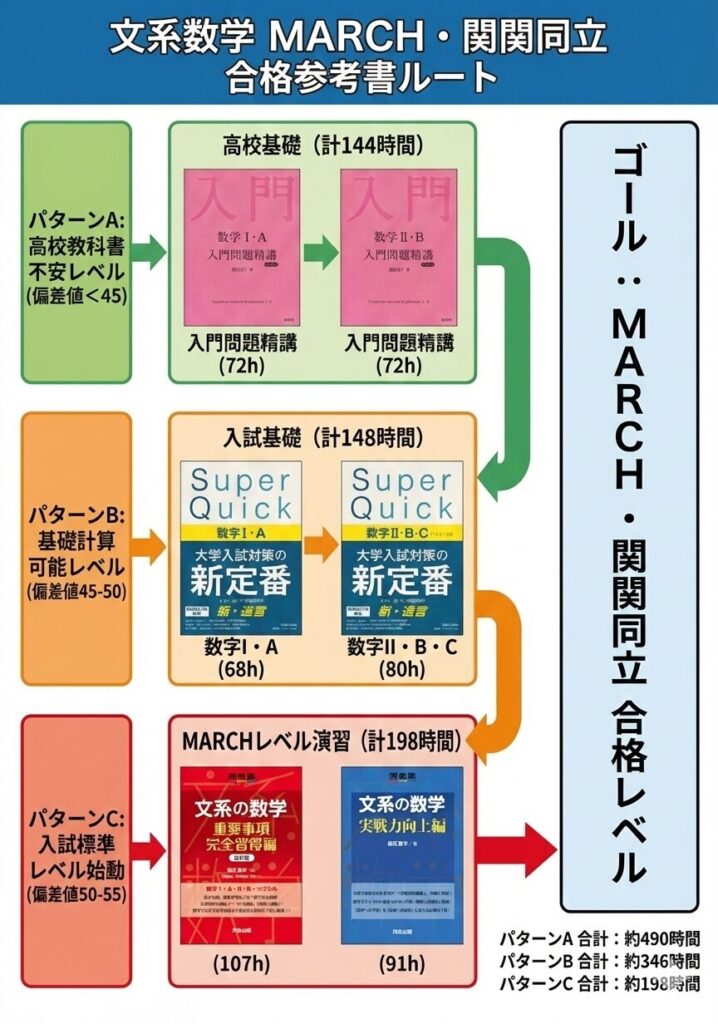
【現状把握】あなたのスタート地点はどこ?(3つのパターン)
まずは自分の現状を客観的に判断しましょう。MARCH・関関同立を目指す場合でも、基礎が抜けていれば必ず戻る勇気が必要です。
| パターン | 現状のレベル感 | 全統模試 偏差値目安 |
| パターンA | 高校教科書 不安レベル 公式の意味が曖昧。定期テストは何とかなるが、模試では全く点が取れない。 | 35 〜 45程度 |
| パターンB | 基礎計算 可能レベル 教科書の例題は解ける。日東駒専レベルの問題にはまだ時間がかかる、またはミスが多い。 | 45 〜 52程度 |
| パターンC | 日東駒専 到達レベル 典型的な入試基礎問題は解ける。しかし、MARCHレベルの「捻った問題」や「融合問題」に対応できない。 | 52 〜 58程度 |
- パターンAの人: 「概念理解」からスタートし、B→Cへと進みます。基礎固めが最重要です。
- パターンBの人: 「入試基礎」からスタートし、Cへと進みます。解法の引き出しを増やします。
- パターンCの人: 「実戦力向上」からスタート。ここからが本当の勝負です。
パターンA:高校数学の概念理解(目安:144時間)
まずは教科書レベルの内容を「なんとなく」ではなく「本質的に」理解するフェーズです。MARCHレベルでは、公式の丸暗記では通用しない問題が出題されます。
使用参考書
- 『数学I・A 入門問題精講』
- 『数学II・B 入門問題精講』


進め方とポイント
- 「なぜそうなるのか?」を追求する: 単に問題を解くだけでなく、解説部分を読み込み、「なぜこの公式を使うのか」を言語化できるようにしてください。
- I・A完了後にII・Bへ: 積み上げ型の科目なので、I・Aの完了を優先します。
学習時間
- 数学I・A:72時間
- 数学II・B:72時間
- 合計:144時間
パターンB:入試基礎の高速処理(目安:148時間)
「分かる」を「できる」に変え、さらに入試標準レベルの問題を「瞬殺できる」状態にします。日東駒専レベルを確実にクリアする実力をつけます。
使用参考書
- 『Super Quick 数学I・A』
- 『Super Quick 数学II・B・C』


進め方とポイント
- スピード重視: 悩んで解くのではなく、問題を見た瞬間に解法が浮かぶまで反復します。
- 計算力の強化: 計算ミスは命取りです。手を動かして、最後まで解き切る訓練を徹底してください。
学習時間
- Super Quick I・A:68時間
- Super Quick II・B・C:80時間
- 合計:148時間
パターンC:難関大演習・実戦力の完成(目安:198時間)
ここがMARCH・関関同立合格へのメインパートです。典型問題(重要事項)を網羅した後、合否を分ける応用問題(実戦力)を攻略します。
使用参考書
- 『文系の数学 重要事項完全習得編』
- 『文系の数学 実戦力向上編』


進め方とポイント
- 2段階構成で攻める:
- まずは『重要事項完全習得編』で、文系入試の頻出パターンを100%にします。ここが完璧でないと、次のステップで挫折します。
- 次に『実戦力向上編』へ進みます。ここはMARCH上位〜早慶レベルも視野に入れた良問揃いです。「別解」や「思考のプロセス」まで熟読し、初見の問題へのアプローチ方法を学びます。
- 解説を読み込む: このレベルの参考書は、問題の裏にある「出題者の意図」を知ることが最大の学びです。
学習時間
- 重要事項完全習得編:107時間
- 実戦力向上編:91時間
- 合計:198時間
各パターンの合計所要時間と学習スケジュール
あなたのスタート地点から、ゴール(パターンC終了)までの総学習時間と期間の目安です。
合計時間と期間の目安
(1日3時間学習した場合)
| スタート地点 | 合計時間 | 期間目安 | 学習の流れ |
| パターンA | 490時間 | 約 5.5ヶ月 | 入門(144h) → Super Quick(148h) → 文系の数学2冊(198h) |
| パターンB | 346時間 | 約 4ヶ月 | Super Quick(148h) → 文系の数学2冊(198h) |
| パターンC | 198時間 | 約 2.5ヶ月 | 文系の数学2冊(198h)のみ |
学習の進め方
- パターンAから: 基礎期間が長くなりますが、焦らず土台を作ってください。ここをスキップすると『文系の数学』に入った瞬間に詰みます。
- パターンBから: まずは『Super Quick』で基礎体力をつけ、後半の約2.5ヶ月で一気に応用力を完成させます。
- パターンCから: すでに基礎がある状態です。『文系の数学』シリーズを徹底的にやり込み、完成度を高めることに集中してください。
このルートを終えた「次」の動き
『文系の数学 実戦力向上編』まで完璧に仕上がれば、MARCH・関関同立の数学で戦える力は十分に備わっています。
- 志望校の過去問(赤本):すぐに過去問演習に入ってください。大学・学部によって「確率」「微積分」「数列」などの頻出分野や、記述式の有無が異なります。形式慣れと時間配分を徹底します。
- 早慶レベルを目指す場合:『実戦力向上編』でも対応可能ですが、さらに高みを目指すなら『プラチカ(文系数学)』などのハイレベル演習書を追加検討します。ただし、多くの文系受験生にとっては、過去問研究を優先する方が得点効率は高いです。
まとめ
MARCH・関関同立の数学は、奇問・難問ばかりが出るわけではありません。「標準的な良問を、いかに落とさず、素早く解くか」が合格のカギです。
- 現状が偏差値45未満なら、迷わず『入門問題精講』から。
- 計算はできるが応用が弱いなら、『Super Quick』で繋ぐ。
- 最後は『文系の数学』2冊で仕上げる。
このルートを信じて進めば、パターンAからのスタートでも約半年弱でMARCHレベルに到達可能です。まずは自分の現在地を認め、最初の一冊を手に取るところから始めましょう。合格へのカウントダウンは、今日から始まります。




コメント